|
O objetivo dessa página é dar uma pequena noção de como é feita a aferição de uma óptica de telescópio refletor.
O newtoniano, o telescópio refletor mais simples, possui um espelho primário côncavo, um secundário de superfície plana e para cada óptica existe um teste específico.
O espelho plano é aferido usando um vidro plano óptico padrão. No caso do espelho primário, é usado um aparelho chamado banco de
Foucault. Durante a fase de polimento, até a finalização da óptica, podem surgir
vários defeitos nos espelhos e para cada um desses defeitos há uma forma correta
de trabalho para eliminar esses problemas. Mais adiante vamos conhecer os
defeitos mais comuns que surgem durante a fase de polimento do espelho.
Banco de Foucault
|
|
|
|
|
Um espelho primário côncavo é aferido por meio de um aparelho chamado banco de Foucault.
Este aparelho possui uma fonte de luz (lâmpada) e uma rede de difração (usada para o chamado teste de Ronchi). A luz atravessa uma fenda e um feixe de luz é enviado para o espelho.
O aparelho (banco de Foucault) é colocado sempre nas proximidades do raio de curvatura do espelho que corresponde ao dobro do valor da distância focal.
Se um espelho possui 1000 mm de distância focal o aparelho é colocado a 2000 mm de distância do espelho.
O espelho reflete então a luz (que passou pela fenda) e chega até a rede de difração. Logo atrás da rede o observador aproxima seu olho para fazer a análise da superfície óptica.
Fotos do banco de Foucault e ao lado esquema animado mostrando o funcionamento do aparelho. |
Noções de espelhos esféricos e parabólicos
|
|
|
|
|
O esquema ao lado mostra o princípio de um espelho esférico que possui uma superfície igual a de uma esfera. No exemplo temos uma grande esfera de vidro
com diâmetro interno de 6 metros.
Uma fonte de luz colocada exatamente no centro da esfera é refletida pela superfície interna e retorna novamente para a fonte de luz (o mesmo ocorre quando colocamos o Foucault no centro de curvatura do espelho).
Assim o espelho esférico nada mais é que uma calota da superfície de uma esfera.
No exemplo a esfera possui 6 m de diâmetro (raio de 3 m) e o raio de curvatura do espelho possui o mesmo valor de 3 m.
A distância focal desse espelho é então de 1,5 metros (metade do valor do raio de curvatura).
Espelhos esféricos aferidos no Foucault.
|
O espelho esférico apresenta o problema
da aberração esférica que deixa a imagem sem nitidez. Nesse caso é preciso
um espelho de superfície parabólica para a correção da aberração esférica.
Mas no caso de telescópios de grande distância focal (ou grande razão focal
- F/D) é possível o uso de espelhos esféricos, pois quanto maior o F/D menor
é a aberração esférica. Para ópticas com F/D menor usamos apenas espelhos
parabólicos.
|
|
|
|
|
Ao lado temos um esquema animado mostrando o princípio de um espelho parabólico.
A superfície do espelho é baseada na forma de uma parábola, diferente do espelho esférico que é baseado em uma esfera..
Vemos que os raios
luminosos refletidos na borda e no centro do espelho encontram o
mesmo ponto do eixo óptico. Podemos dizer que um espelho
parabólico possui diversos raios de curvatura, pois a luz
refletida em cada área do espelho encontra o eixo óptico no
mesmo ponto focal e dessa forma ocorre a correção da aberração
esférica.
Espelho parabólico no teste de Ronchi e no teste de Foucault.
|
À medida que diminuímos a razão focal (F/D menor) é preciso uma superfície mais parabólica para a correção da aberração esférica.
Um espelho F/D=7 possui uma parábola leve. Já um primário F/D=6 apresenta uma parábola mais acentuada que o F/D=7 e assim por diante.
Quanto menor a razão focal (F/D) maior será a parábola do espelho.
 |
|
|
|
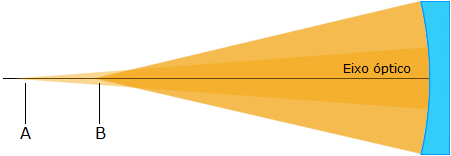
Nos espelhos esféricos a luz refletida
em áreas diferentes do espelho encontram o eixo óptico também em
pontos diferentes. O esquema ao lado mostra a luz refletida na
borda do espelho encontra o eixo óptico no ponto B. Já a luz
refletida no centro encontra o eixo óptico no ponto A.
Essa diferença de posição dos raios de luz, com o eixo óptico,
provoca a chamada aberração esférica. Quanto maior a distância focal do espelho, menor a aberração esférica.
|
Testes ópticos
Como referência vamos usar um espelho esférico para mostrar as formas e defeitos que óptica pode adquirir durante a fase polimento.
Como são mais simples, os espelhos esféricos são indicados para quem deseja fazer sua primeira óptica.
 |
|
|
|
A figura 1 mostra o aspecto de um espelho esférico pelo teste de Ronchi com as linhas retas e paralelas.
À direita o perfil do espelho com sua superfície côncava.
Na figura 2 temos a chamada superfície de forma esferóide oblato quando as linhas se curvam na direção do centro do espelho.
O desenho azul mostra o perfil do espelho. A linha vermelha mostra o defeito na superfície indicando que o espelho está elevado em toda a sua área.
A figura 3 mostra o inverso onde as linhas se curvam na direção da borda do espelho e nesse caso temos o espelho parabólico.
Para um espelho de grande distância focal (esférico) essa configuração é errada, pois a aberração esférica criada é muito grande diminuindo a qualidade óptica.
Na imagem azul, à direita, a linha vermelha mostra o defeito na óptica onde toda a superfície está mais funda.
A figura 4 mostra o defeito conhecido como " borda caída " onde as linhas se curvam bastante na borda do espelho.
A imagem em azul (que representa o perfil do espelho) mostra a borda do espelho caída.
Uma borda caída de vários milímetros é considerado um defeito grave, pois pode provocar perda na qualidade da imagem.
A figura 5 mostra uma depressão no centro do espelho. Apenas a parte central está mais funda que o restante da superfície.
Já a figura 6 mostra o inverso, uma elevação na região central. Nesse caso o centro está mais elevado que o restante da superfície.
Todos os desenhos azuis (espelho visto de lado) estão representados de forma exagerada.
Não é possível ver estes defeitos apenas olhando para o espelho.
Estes defeitos (e muitos outros) são apenas visíveis analisando os espelhos com o banco de Foucault (teste de Ronchi ou teste da parábola com um micrômetro).
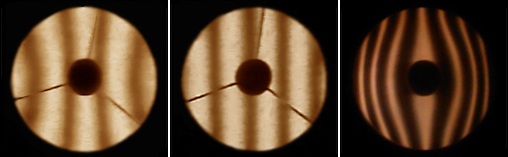
Exemplos
de óptica esferóide, esférica e parabólica.
|
Podemos aferir a óptica de um telescópio colocando uma rede
de difração diretamente no focalizador (sem a ocular).
Ao apontar o telescópio para uma estrela (ou uma fonte de luz bem distante) a rede de difração produzirá várias linhas.
O ideal são linhas retas e paralelas como mostram as 3 imagens abaixo (a partir
da esquerda) de um Schmidt Newtoniano.
Uma pequena curva nas linhas não significa que o telescópio possui uma óptica ruim. A
última imagem, à direita, mostra a superfície de um espelho feito pelo teste de Ronchi.
É possível perceber diversos defeitos como borda caída acentuada, o centro com uma leve depressão, grande rugosidade nas linhas e etc.
Essa foto foi retirada do livro "How to Make a Telescope" e segundo o autor, Jean Texereau, a combinação de defeitos não altera seriamente a imagem e é algo que passa despercebido observando uma estrela.
Conjunto óptico com grande correção e óptica com diversos defeitos.
Planos Ópticos (espelhos planos)
A análise de um espelho plano é mais complexa se comparado com o espelho primário. Para esse espelho não é usado o aparelho de Foucault,
pois este somente é usado em espelhos côncavos.
É necessário, para a análise, um vidro plano de excelente qualidade óptica,
conhecido como padrão óptico. Sobre o vidro que será aferido é colocado o
padrão. Em seguida usamos uma fonte luminosa apropriada que permite então a
aferição do espelho. As duas superfícies em contato produzem linhas que são
interpretadas de modo semelhante nos espelhos primários. Nesse caso
um bom espelho plano deve apresentar linhas retas e paralelas. Quando o espelho
possui baixa qualidade o resultado obtido é diferente. Podem surgir vários
círculos (que indica primeiramente que o espelho está muito côncavo ou convexo)
ou mesmo linhas muito irregulares indicando total falta de qualidade (superfície
ondulada). As 3 primeiras imagens abaixo mostram um vidro plano comum de 200 mm de diâmetro e 12 mm de espessura.
As outras 2 fotos (à direita) superfície óptica de grande precisão com linhas retas e paralelas.
Vidro comum sem precisão (linhas irregulares) e vidro de grande precisão com linhas retas.
Sequência de fotos que mostram o teste no espelho terciário do telescópio ETX 90 da Meade.
Neste caso não temos linhas retas e sim linhas com uma curvatura ou dois anéis como mostra a
última foto à direita.
Isso não significa que o espelho não possui qualidade óptica e os anéis indicam que o espelho possui uma curvatura mais acentuada se comparado com um espelho de linhas retas.
Espelho terciário plano do telescópio Meade ETX 90.
| 
